Problem 2-1, Comparing a single mean to a specified value

Problem statement

The breaking strength of a fiber is required to be at least 150 psi. Past experience has indicated that the standard deviation of breaking strength is σ = 3 psi. A random sample of four specimens is tested, and the results are y₁ = 145, y₂ = 153, y₃ = 150, and y₄ = 147.

1. State the hypotheses that you think should be tested in this experiment.
2. Test these hypothesis using α = 0.05. What are your conclusions?
3. Find the P-value for the test in part (b).
4. Construct a 95 percent confidence interval on the mean breaking strength.

Solution

Figure 1: Our data compared to a theoretical Gaussian distribution.

Section A: Choosing hypotheses

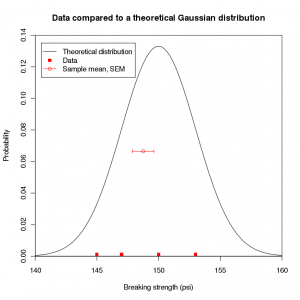
In this problem we are given a set of four data points. These data points all come from a distribution of breaking strengths which has an unknown mean μ. We will call this the true distribution. Previous experience indicates that breaking strengths follow a Gaussian theoretical distribution with a standard deviation of 3 psi, so we assume this for our distribution also. Our task is to determine whether or not the true mean, which is impossible to know exactly, is greater than or equal to 150 psi. We plot this data and the distribution in figure 1.

Since the sample mean is an approximation of the true mean, we define the standard error of the mean (SEM) to be $\sigma /{\sqrt {n}}=1.5$, where n=4 is the number of data points.

	Distribution type	Mean	Standard deviation
True distribution	Normal	$\mu \approx {\overline {y}}=148.25$	$\sigma =3$
Theoretical distribution	Normal	$\mu _{0}=150$	$\sigma _{0}=3$

We first state two hypotheses. The null hypothesis is that our data does come from the theoretical distribution: the true mean μ = μ₀. Our alternative hypothesis states that the data comes from a distribution centered around a different mean.

There are three choices for the alternative hypothesis: μ < 150, μ > 150, and μ ≠ 150. We adopt the convention that the alternative hypothesis will be true if the data does not meet the requirements. In this case, the breaking strength of the fiber is required to be at least 150 psi, so we choose μ < 150 as our alternative hypothesis.

Formally, we state our hypotheses as:

H₀: μ = 150
H₁: μ < 150

Figure 2: Our plot after normalizing.

Section B: Z-values

For convenience, we start by standardizing our theoretical distribution to have a mean of zero and a standard deviation of one. To do this, we first center the distribution around zero by subtracting the theoretical mean (150) from each point in the distribution. We then divide each point by the standard deviation (3). The sample mean can be standardized in the same manner. We plot the normalized distribution and sample mean in figure 2.

We now assume that the null hypothesis is true and ask whether or not this assumption makes sense. Given that this assumption is true, the sample mean is most likely to be close to zero. To test this, we define a range over which we consider our sample mean to be unacceptable, the rejection region. If the sample mean is in the rejection region, it is too far from zero and we reject the null hypothesis.

We will define the lower limit to be z_α, where α=0.05. Graphically, given a standard Gaussian distribution, the area under the curve left of z_0.05 is equal to 5% of the total area. You can either look up z_α in a table or calculate it using a software package. Using Excel, the appropriate function is =NORMSINV(alpha). The corresponding function in R is qnorm(alpha). Using one of these methods, we find that z_0.05=−1.64.

We then find the z-value of our data and compare the z-value to z_α. The formula for the z-value is as follows:

$z=({\overline {y}}-\mu _{0})({\frac {1}{\sigma }})({\sqrt {n}})$

Because we have already standardized our data, μ₀=0 and σ=1, so this formula simplifies to ${\overline {y}}{\sqrt {n}}=-0.417\cdot 2=-0.833$. Note that the formula above normalizes the data, if it has not already been normalized. The z-value can be interpreted as the distance between the sample mean and μ₀, scaled by a factor which makes the z-value more extreme with large sample sizes. If we take many samples, our z-value is more likely to fall in the rejection region, because we are more certain of the accuracy of our sample mean.

The rejection region for our z-value is from negative infinity to z_α. We see that our z-value is greater than z_α. Therefore, we cannot reject the null hypothesis.

Figure 3: Illustrating the P-value.

Section C: P-values

Another way to judge how likely it is that our null hypothesis is true is to calculate the P-value. If we were to redo the experiment, taking four new data points, the P-value gives us the probability of our new sample mean being at least as extreme as our original sample mean. Graphically, if we extend the critical region until it reaches our z-value, the P-value is equal to the area of the shaded region (see figure 3).

To calculate the P-value in Excel, use =NORMSDIST(-ABS(z)). In R, use pnorm(-abs(z)). (We use the negative absolute value because NORMSDIST and pnorm integrate from negative infinity to the z-value. If the z-value is positive, we instead want to integrate from the z-value to positive infinity, which is mathematically equivalent to integrating from negative infinity to the negative of the z-value.)

For this problem, we find that the P-value is 0.202. Note that a P-value of 0.5 indicates that the sample mean is equal to the mean of the theoretical distribution. You can see this graphically by noting that the z-value will be zero in this case, and integrating the theoretical distribution to zero covers half of the area. (Recall that the total area under a standard Gaussian curve is one.) The further the P-value is from 0.5, the greater the distance between the two means.

Figure 4: The confidence interval about the sample mean.

Figure 5: The confidence interval about the theoretical mean.

Section D: Confidence intervals

We now return to our original data set and theoretical distribution with the mean of 150 psi; that is, we will no longer use our normalized space.

We will now calculate the range of sample means that would lead us to conclude that the breaking strength of our fiber is at least 150 psi, given an α of 0.05. This range is known as the confidence interval about the sample mean.

To calculate this interval, we ask what sample mean would give us a z-value equal to z_α. We can determine this by substituting z_α for z into the formula for z, and solving for ${\overline {y}}$:

$z_{\alpha }=({\overline {y}}-\mu _{0})({\frac {1}{\sigma }})({\sqrt {n}})\Rightarrow {\overline {y}}=\mu _{0}+{\frac {z_{\alpha }\sigma }{\sqrt {n}}}=147.53$

This is the lower limit of our confidence interval. Because any sample mean greater than 150 is acceptable, the upper limit of the confidence interval is infinity. We plot this interval in figure 4. Formally, our confidence interval about the sample mean is

$147.53<{\overline {y}}<\infty$

We next calculate a confidence interval about the mean of the theoretical distribution, μ₀. This will give us the range of minimum breaking strengths we could have specified and still found our data acceptable. We can calculate this in much the same way as the previous confidence interval: substitute z_α for z in the formula for z, but this time solve for μ₀:

$\mu _{0}={\overline {y}}-{\frac {z_{\alpha }\sigma }{\sqrt {n}}}=151.22$

This is the upper limit of our confidence interval. The lower limit is zero, because we simply require the theoretical mean to be less than this number. Formally, our confidence interval about the theoretical mean is

$0\leq \mu _{0}<151.22$